最高のコレクション 1^2 2^2 3^2 .... n^2 = n(n 1)(2n 1)/6 untuk setiap bilangan asli n 152896

Nov 17,  · Ex 41,2 Prove the following by using the principle of mathematical induction 13 23 33 n3 = ( ( 1)/2)^2 Let P (n) 13 23 33 43 n3 = ( ( 1)/2)^2Contoh lainnya Setiap bilangan bulat positif n (n 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan= () () Sebagai contoh, !

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 2

1^2 2^2 3^2 .... n^2 = n(n 1)(2n 1)/6 untuk setiap bilangan asli n

1^2 2^2 3^2 .... n^2 = n(n 1)(2n 1)/6 untuk setiap bilangan asli n-Jika n bilangan asli maka n faktorial (n!) didefinisikan dengan n!Efek domino tidak hanya berlaku untuk kepingkeping yang sama besarnya Pada tahun $01$, seorang fisikawan dari Exploratorium San Fransisco, melakukan eksperimen dengan membuat keping domino dari kayu lapis sebanyak $8$ keping, masingmasing $50\%$ lebih besar dari keping sebelumnyaKeping yang pertama ukurannya $5$ cm, keping yang kedua ukurannya $7,5$ cm

Induksi Matematika Ppt Download

Contoh Soal Gunakan induksi matematik untuk membuktikan bahwa jumlah n buah bilangan ganjil positif pertama adalah n 2 Penyelesaian Basis induksi Untuk n= 1, jumlah satu buah bilangan ganjil positif pertama adalah 1 2 = 1 Ini benar karena jumlah satu buah bilangan ganjil positif pertama adalah 1Bab 2 BARISAN BILANGAN REAL by Julan HERNADI Exercise 4 Gunakan de nisi limit barisan untuk membuktikan lim 3n1 2n5 = 3 2 enTtukan bilangan asli terkecil N yang dapat diambil jika diberikan "= , juga4Buktikan dengan induksi matematika bahwa untuk setiap bilangan asli n, 72n1 1 habis dibagi oleh 8 5Buktikan dengan induksi matematika bahwa untuk setiap bilangan asli n, 2 4n3 3 3n1 habis dibagi oleh 11

1 Prove that n2 1 2n when n is a positive integer with 1 n 4 n 1 n2 1 1 1 2 2 2 from LOGMAT MSH1 at Telkom University, Bandung Prove that n2 1 ≥ 2n when n is a positive integer with 1 ≤ n ≤ 4 n = 1 →n 2 1 = 1 1 = 2 ≥ 2 = 2 1 = 2 n n = 2 Sebagian x, semua y dimana P(y) jika dan hanya jika x sama dengan y b Sebagian xBuktikan dengan induksi matematika sederhanabahwa untuk setiap nbilangan asli berlaku1^32^33^3 n^3=0,25 n^2(n1)^2Sep 26, 10 · Untuk n = 1 akan diperoleh 1 = 1² > 1 = 1 Induksi misalkan untuk n = k asumsikan 1 3 5 (2k – 1) = k² Untuk n = k 1 berlaku

= n x (n1) x (n2) x (n3) x x 3 x 2 x 1 Dari definisi itu, maka kita juga memeroleh n!Bernilai 7 × 6 × 5 × 4 × 3 × 2Solution For For all n \in N , 1 ^ { 2 } 2 ^ { 2 } 3 ^ { 2 } 4 ^ { 2 } \cdots n ^ { 2 } = \dfrac { n ( n 1 ) ( 2 n 1 ) } { 6 } 500 150 For all n ∈ n ∈

Induksi Matematika Matematika

Buktikan Pernyataan Pern Descubre Como Resolverlo En Qanda

Solution for n/22=3 equation n/22=3 We move all terms to the left n/22(3)=0 We add all the numbers together, and all the variables n/21=0 We multiply all the terms by the denominator n1*2=0 We add all the numbers together, and all the variables n2=0 We move all terms containing n to the left, all other terms to the right n=2Jul 21,  · A(n) 2 4 6 2n = n(n1), untuk setiap nilai n adalah bilangan asli Pembuktian pernyataan matematika dapat dilakukan dengan induksi matematika dengan 2 langkah yaitu basis induksi dan langkah induksi1 Akan ditunjukkan bahwa 5n 1 habis dibagi 4 untuk n = 1 Jelas sekali bahwa 51 1 = 5 1 = 4 habis dibagi 4 2 Asumsikan bahwa 5n 1 habis dibagi 4 untuk n = k, yaitu 5k 1 habis dibagi 4

Definisi Induksi Matematika Adalah Ppt Download

1 Dengan Menggunakan Indu Lihat Cara Penyelesaian Di Qanda

Simple and best practice solution for N/21n/5=1/2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so= 1 Sebagai contoh, 7!0 = 2n 2 – 4n – 6 0 = n 2 – 2n – 3 0 = (n – 3)(n 1) Jadi n = 3 Sehingga 11 adalah suku ke 3 03 Pada barisan bilangan segitiga tentukanlah (a) Suku ke 6 (b) Jumlah delapan suku pertama Jawab Menurut rumus barisan bilangan segitiga 1, 3, 6, 10, 15, Un = ½ n (n1) Sn = ⅙ n (n1) (n2) Sehingga a U 6 = ½ (6) (61) = 3

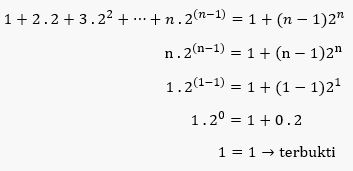
Contoh Soal Induksi Matematika Untuk Semua Bilangan Asli N

Contoh Soal Induksi Matematika Dan Jawaban Pembahasan

Karena n bilangan bulat ganjil, maka kita bisa tuliskan sebagai n = 2k 1, untuk semua bilangan bulat kSelanjutnya kita perhatikan 2 = (2 1) 2 = 4 2 4k 1 = 2(2 2 k) 1Kita misalkan m = 2 2 k , sehingga menjadi 2 = 2m 1 (ini merupakan bentuk dari bilangan bulat ganjil)Jadi pernyataan tersebut terbukti ∎ b= = Nilai 0!Induksi Matematik Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik Contoh Misalkan p(n) adalah pernyataan yang menyatakan "Jumlah bilangan bulat positif dari 1 sampai n adalah n(n 1)/2" Buktikan bahwa p(n) benar!

1 3 6 N N 1 1 6n N 1 N 2 Mas Dayat

Induksi Matematika

Buktikan bahwa (n1) 2Aug 17,  · yang sama persis dengan hasil manipulasi aljabar di atas Sehingga dapat disimpulkan bahwa pernyataan benar untuk n=k1 Kesimpulan Pernyataan 2 n2 n1 =1(n1)2 n untuk n semua bilangan asli, memenuhi 2 syarat induksi matematika, sehingga pernyataan tersebut terbukti benar1^22^23^2n^2=1/6 n(n1) (2n1)=

Outline Definisi Prinsip Induksi Sederhana Ppt Download

Soal Latihan Fondasi Induksi

Jadi terbukti bahwa n(n 1)(n 2) habis dibagi 3 untuk n bilangan asli 08 Buktikanlah bahwa untuk n ≥ 4 dan n bilangan asli berlaku 3 n > n 3 Jawab Ambil n = 4 maka 3 4 > 4 3 artinya 81 > 64 (bernilai benar) Ambil n = 5 maka 3 5 > 5 3 artinya 243 > 125 (bernilai benar) Ambil n = 6 maka 3 6 > 6 3 artinya 729 > 216 (bernilai benar)Dengan kata lain, barisan dalam ℝ mengawankan setiap bilangan asli n =1,2,3, kepada suatu bilangan real, jika X ℕ ℝ merupakan barisan, maka biasanya dituliskan dengan nilai dari X pada n dengan notasi Barisan sering dinotasikan dengan X atau ( ) atau( ∶ ∊ ℕ) atau { } atau { }( ≥ 1)apabila diketahui suatu barisan Y , artinya Y2n 1 untuk setiap n = 1;2;

Latihan Soal

Contoh Soal Induksi Matematika

= 1 Jadi, untuk 0!$1^2 2^2 3^2 \cdots n^2 = \dfrac{1}{6}n(n 1)(2n 1)$ terbukti 5 {2n 1}$ adalah 5, untuk setiap n bilangan asli Langkah 1 Untuk n = 1 $2^{2n 1} 3^{2n 1} = 2^{21 1} 3^{21 1}$ $= 8 27 = 35 = 57$ → 5 adalah salah satu faktor Rumus atau teorema benar untuk n = 1Sehingga p13 ǀ (a13 b13 ) Sehingga diperoleh pn ǀ (a13 b13 ) untuk setiap bilangan asli n ≤ 13 Jadi, banyak bilangan asli n ≤ 13 sehingga a13

Ppt Induksi Matematika

Pdf Kal 3 Barisan Bilangan Real Hediana Lukmawati Academia Edu

Karena langkah 1 dan 2 keduanya telah diperlihatkan benar, maka untuk semua bilangan bulat tidaknegatif n, terbukti bahwa 2 0 2 1 2 2 13 2 n = 2 n 1 – 1¾ 5 Untuk tiap n ≥ 3 jumlah sudut dalam sebuah poligon dengan n sisi adalah 180( n − 2)°Buktikan dengan induksi matematika sederhanabahwa untuk setiap nbilangan asli berlakuinduksi matematika , 1^22^23^2(1)^(n1)n^2=0,5 (1)^(n1)n(n1)Preview this quiz on Quizizz Diketahui suatu barisan aritmetika denganU5 = 7 dan U8 = 13 Suku ke adalah

Doc Kumpulan Soal Jawab Olimpiade Matematikadaripertemuan Berau Putri Utiw Academia Edu

Matematika Pernyataan Ber Lihat Cara Penyelesaian Di Qanda

B = 1 (bilangan asli) Un = 210 Kita cari nilai n Un = a (n1) b 210 = 11 (n1) 1 210 = 11 n – 1 n = 0 Selanjutnya kita cari nilai Sn S n = n/2 (a U n) = 0/2 () = 100 x 221 = Jadi jumlah bilangan asli berurutan mulai dari 11 sampai dengan 210 adalahJumlah n bilangan asli kuadrat pertama adalan 12 22 32 n2 = ( n(n1)(2n1) ) / ( 6 ) Di dalam lingkaran yang berdiameter cm terdapat sebuah juring dengan besar sudutpusat 450 Luas juring tersebut adalahDalam matematika, Faktorial dari bilangan bulat positif dari n yang dilambangkan dengan n!, adalah produk dari semua bilangan bulat positif yang kurang dari atau sama dengan n !

Induksi Matematika Materi Lengkap Matematika

1 3 2 3 3 3 N 3 1 4n 2 N 1 2 Buktikan Dengan Induksi Matematika Sederhana Bahwa Setiap N Brainly Co Id

N (n 2 1) habis dibagi 3 4 Buktikan bahwa P n ≡ 7 2 n − 1 3 2 n habis dibagi 8 untuk setiap bilangan asli n 5 Untuk setiap n bilangan asli, buktikan bahwa 2 n ≥n 1Nov 12, 18 · c 1^2 2^2 3^2 n^2 = n(n1(2n1)/6, untuk setiap bilangan asli n d 1^3 2^3 3^3 n^3 = (1 2 3 n)^2 ,untuk setiap bilangan asli n e 12 23 34 n (n1 ) = n (n1 ) (n 2) per 3 untuk setiap bilangan asli Jawab a Dalam pembuktian dengan menggunakan induksi matematika ada dua langkah yaitu 1Buktikan untuk setiap bilangan asli n ≥ 2 berlaku 3 n > 1 2n Jawab Langkah Pertama Akan ditunjukkan n=(2) benar 3 2 = 9 > 1 22 = 5 Jadi, P(1) benar Langkah Kedua Asumsikan n=(k) benar, yaitu 3 k > 1 2k, k ≥ 2 Langkah Ketiga Akan ditunjukkan n=(k 1) juga benar, yaitu 3 k1 > 1 2(k 1) 3 k1 = 3(3 k)

Membuktikan Dengan Induksi Matematis Buktikan Bahwa Pernyataan Berikut Bernilai Benar A 1 2 2 2 Brainly Co Id

Matematika Diskret Induksi Matematik Diskret Induksi Matematik Untuk Semua N T 1 N 3 2 N Pdf Document

Analisis Real (Barisan Bilangan Real) Latihan bagian 22 1 Latihan Bagian 22 (Hal 43) 1 Selidikilah barisan 𝒳 = (𝒳n) berikut divergen/konvergen jika (a) xn = n n1 (b) xn = (−1)n n n1 (c) xn = n2 n1 (d) xn = 2n2 3 n21 Penyelesaian (a) lim n→∞ xn = lim n→∞ n 1 n n=1 1 n = lim n→∞ 1 1 1 n = lim 1 lim 1 lim 1 n = lim 1 lim 1 = 1 Maka divergen (b) lim nUntuk sebarang bilangan asli k, Jika P(n) bernilai benar untuk n=k, buktikan P(n) bernilai benar untuk n = k1Soal 3 Menggunakan Induksi Matematika Buktikan bahwa untuk setiap bilangan bulat positif n, Pembahasan Misalkan P(n) adalah pernyataan 1 2 3 n = n(n 1)/2 Kita akan menunjukkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n Kita harus menunjukkan bahwa P(1) benar

Contoh Soal Induksi Matematika Dan Jawaban Pembahasan

7 Induksi Matematika Ppt Download

Aug 14,  · Jawab Pada pembahasan pembuktian langsung dan tidak langsung aku udah jelasin mengenai bentukbentuk bilangan ganjil dan genap Agar kamu gak bingung sebaiknya pahami dulu materi tersebut Kita harus ubah dulu pernyataan di soal kedalam bentuk rumus matematikanya "jumlah bilangan genap" artinya semua bilangan genap dijumlahkan hasilnya akan sama dengan rumus \(n^{2}nAug 08, 18 · Cek untuk n = 1 Dari rumus jumlah diatas, yaitu yang di ruas kanan, kita gunakan dulu n = 1 Tujuannya untuk membuktikan suku pertama yang ada dikiri sama atau tidakAdalah 1, menurut konvensi untuk produk kosong Operasi faktorial digunakan sebagai bidang matematika, terutama di kombinatorik, aljabar, dan analisis matematika

1 2 3 N 1 6n N 1 2n 1 Induksi Matematika Brainly Co Id

Proof 1 2 3 N N N 1 2n 1 6 Youtube

Click here👆to get an answer to your question ️ n Lt→∞ 1 4 9 n^2/n^3 =Dalam matematika, notasi Sigma adalah penjumlahan dari suatu urutan bilangan apa pun, hasilnya adalah jumlah atau total mereka Selain bilangan, tipe nilai lainnya dapat dijumlahkan juga fungsi, vektor, matriks, polinomial dan, secara umum, anggota dari semua jenis objek matematika di mana operasi yang dilambangkan "" didiefinisikan Penjumlahan tak hingga disebut deret tak hingga2 Metode pembuktian untuk proposisi yang berkaitan dengan bilangan bulat adalah induksi matematik Contoh 1 Buktikan bahwa jumlah n bilangan bilangan bulat positif pertama adalah n(n 1)/2 2 Buktikan bahwa jumlah n buah bilangan ganjil positif pertama adalah n2 Rinaldi Munir/IF21 Matematika Diskrit

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 2

Induksi Matematika Buktikan 1 2 3 N 1 6 N N 1 2n 1 Brainly Co Id

= 1 Oleh karena itu, untuk n = 1, diperoleh 1!Kết quả ra là 1 hàm đa thức theo n gửi về địa chỉ email protected, ĐT đê nhận thưởng vể diễn đàn chính /thông tin toán học , xem chương trình giải toán có thưởng Giải thưởng thìJun 22, 17 · Please see below Induction method is used to prove a statement Most commonly, it is used to prove a statement, involving, say n where n represents the set of all natural numbers Induction method involves two steps, One, that the statement is true for n=1 and say n=2 Two, we assume that it is true for n=k and prove that if it is true for n=k, then it is also true for n=k1

Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian

Contoh Soal Induksi Matematika Docx Contoh Soal Induksi Matematika Jawaban Pembahasan Lengkap Soalkimia Com Contoh Soal Induksi Matematika Dan Kunci Course Hero

Oct 22, 19 · Soal Induksi Matematika, Buktikan n4 – 4n2 habis dibagi 3, untuk semua bilangan bulat lebih >=2 Langkah Basis Induksi, Untuk n=2 , maka n4 – 4n2 = 24 – 422 =16 – 16 = 0 hasilnya =0, angka 0 dibagi 3 adalah 0 Langkah Induksi, untuk n 1, makaJadi dengan menggunakan Prinsip Induksi Matematika kita dapat menyimpulkan bahwa P(n) benar untuk semua bilangan bulat n ≥ 2 Soal 10 Membuktikan Faktor Buktikan bahwa 3 adalah faktor 4 n – 1 untuk semua bilangan bulat positif n Pembahasan Untuk n = 1, pernyataan tersebut benar karena Sehingga, 3 adalah faktor bentuk di atasKarena x6 = 1 21 213 214 , maka untuk n = 3 2 Karena x4 = 1 (2 2 213 215 Secara umum, dengan menggunakan induksi matematika dapat dibuktikan bahwa setiap bilangan asli n berlaku diperoleh x7 = 1 1 2 x2n1 = 1 =1 1 1 1 1 3 5 2n−1 2 {z 2 } 2 2 1 (1 2 deret geometri n suku − ( 14 )n ) 3 4 n

Dengan Induksi Matematika Buktikan Rumus Benar Untuk Semua N Bilangan Asli 2 4 8 2 N Brainly Co Id

Induksi Matematika Teobil

3n1 2n5 ¶ = 3 2 Tentukan bilangan asli terkecil N yang dapat diambil jika diberikan "= , juga bila "= hingga jxnj • M untuk setiap n 2 N Dengan kata lain, barisan (xn) terbatas Contoh 221 Barisan (1=n n 2 N)Dengan induksi matematik, buktikan bahwa untuk bilangan asli n berlaku 42n1 3n2 habis dibagi 13 Problem Dengan menggunakan induksi matematik buktikan bahwa untuk setiap bilangan asli n berlaku 311 (8n 5) = 4n2 n Problem Misalkan a bilangan real dan a 6= 1 Dengan induksi matematik, tunjukkan bahwa 1aa2 an 1 = 1 an 1 a untuk setiapGiải thưởng iphone 5 cho ai tính được 1 k 2 k 3 k n k =?

Induksi Matematika Materi Lengkap Matematika

Induksi Matematika 1 2 2 2 3 2 1 N 1 N 2 0 5 1 N 1 N N 1 Youtube

Contoh 12 Gunakan induksi matematika untuk membuktikan bahwa 5n 1 dapat dibagi 4 untuk setiap n = 1;2;

How To Prove With Mathematical Induction That 1 3 2 3 3 3 N 3 N 2n 1 3 N 1 3 4 Quora

2 4 6 8 2n N N 1 Setiap Bilangan Asli

Soal Induksi Matematika Brainly

Contoh Soal Induksi Matematika Sederhana Brainly Soal Soal

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 2

Induksimatematika Sumire

3 Buktikan Dengan Induksi Ma See How To Solve It At Qanda

Dengan Menggunakan Prinsip Induksi Matematika Buktikan Bahwa 2 4 6 8 2n N N Untuk N Brainly Co Id

Contoh Soal Induksi Matematika Dan Jawaban Pembahasan

Buktikan N N 1 N 2 Habis Dibagi 6 Matematika2

How To Prove With Mathematical Induction That 1 3 2 3 3 3 N 3 N 2n 1 3 N 1 3 4 Quora

Bab I Induksi Matematik Induksi Matematik Merupakan Salah

Contoh Soal Induksi Matematika Kelas 11 Beserta Jawabannya Tekape Id

Soal Latihan Fondasi Induksi Matematika

Induksi Matematik

Induksi Matematika Oleh Sri Supatmi S Kom Rinaldi

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 2

Kumpulan Soal Jawab Olimpiade Matematika

Contoh Soal Induksi Matematika Sederhana Brainly Soal Soal

Buktikan N3n Untuk Setiap Lihat Cara Penyelesaian Di Qanda

Principio De Induccion Ejercicio 1 3 2n 1 N 2 Youtube

Pdf Induksi Matematika

Prove That 1 3 5 2n 1 N 1 2n 1 2n 3 3 Whenever N Is A Nonnegative Integer Homework Help And Answers Slader

Ex 4 1 8 Prove 1 2 2 22 3 23 N 2n N 1 2n 1 2

Induksi Matematika 1 3 2 3 3 3 N 3 0 25 N 2 N 1 2 Youtube

7 Induksi Matematika Ppt Download

Soal Induksi Matematika Teorema Binomial Beserta Jawabannya

Induksi Matematika

25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 5

Buktikan Induksi Matematika 2 4 6 2n N N 1 Brainly Co Id

4n 2n Untuk Semua Bilangan Bulat Positif N 5 Mas Dayat

Buktikan Bahwa Pernyataan Berikut Bernilai Benar 2 4 6 8 2n N N 1 Untuk Setiap Bilangan Asli Brainly Co Id

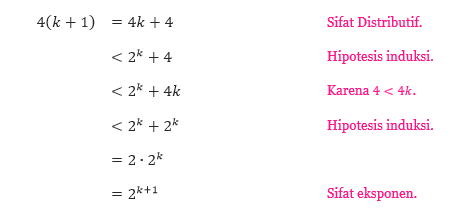
25 Soal Dan Pembahasan Induksi Matematika Pendidikan Matematika Laman 3

Induksi Matematika

Uh Induksi Matematika 17 18

Induksi Matematika Materi Contoh Soal Pembuktian

Analisis Real Barisan Bilangan Real Latihan Bagian 2 1

Membuktikan Dengan Induksi Matematis Youtube

Ex 4 1 5 Prove 1 3 2 32 3 33 N 3n 2n 1 3n 1

Induksi Matematika Ppt Download

Induksi Matematik

Dengan Mengikuti Langkah Lihat Cara Penyelesaian Di Qanda

Teori Bilangan

Induksi Matematika

Ex 4 1 5 Prove 1 3 2 32 3 33 N 3n 2n 1 3n 1

Gunakan Induksi Matematika Untuk Membuktikan Bahwa 1 2 2 2 2 Pangkat 4 2 Brainly Co Id

Induksi Matematika 3 6 12 3 2 N 1 3 2 N 1 Youtube

Matematika Wajib Kelas Xii By Abdullah Sman 1 Genteng Issuu

Pdf Soal Soal Olimpiade Matematika Dan Penyelesaiannya Ary Brainer Academia Edu

Matematika Dasar I Dosen Asri Nur Chiquita Himpunan

Dilarang Kirim Rep Oot در توییتر Tanyarl Ada Yg Bisa Tolongin Bantu Jawab Soal Yg Dilingkari Ga Itu Materi Mtk Ttng Induksi Kls 11 Makasiii

Induksi Matematika Prinsip Pembuktian Deret Keterb

Buktikan Bahwa Untuk Setiap Bilangan Asli N Berlaku 1 2 3 N 1per2 N N 1 Brainly Co Id

Induksi Matematika

Induksi Matematika Makalah Prinsip Dan Contoh Soal

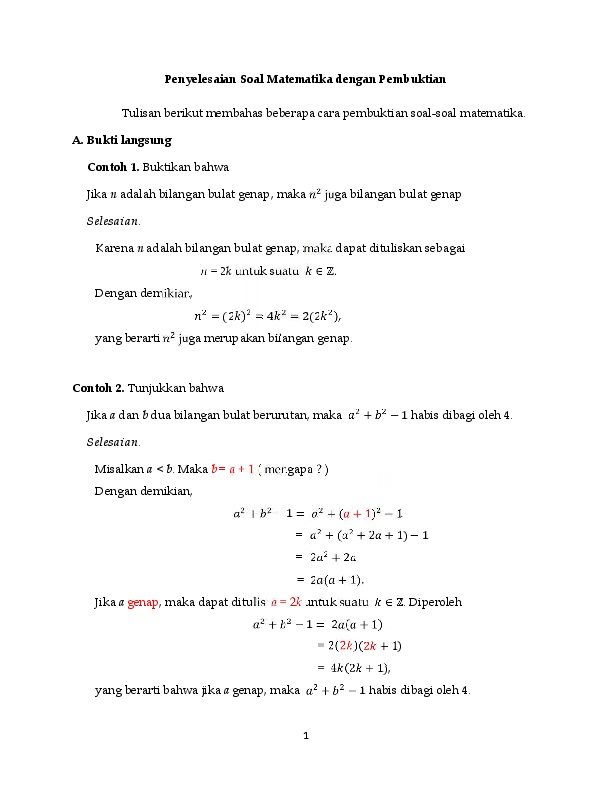
Pdf Penyelesaian Soal Matematika Dengan Pembuktian Kusuma Hadi Purnawan Academia Edu

2 4 6 8 2n N N 1 Untuk Setiap Bilangan Asli N Induksi Matematis Brainly Co Id

Contoh Soal Induksi Matematika Habis Dibagi 2 Soal Soal

4 Dfrac112dfrac123dfrac13 Lihat Cara Penyelesaian Di Qanda

Induksi Matematika Ppt Download

1 2 2 3 3 4 N N 1 1 3 N N 1 N 2 Mas Dayat

Induksi Matematika